Abstract Therefore, previous research has utilized predictive models of athletic performance as a benchmark for guiding athlete training, management14, and strategic planning in sports teams15. For example, researchers have built such models to evaluate motor control and stability to provide runners with precise training recommendations16. In addition, studies that predicted sports performance from a four-dimensional […]

Abstract
Introduction
Google Scholar
S Sanjaykumar K Udaichi G Rajendiran M Cretu Z Kozina 2024 Cricket performance predictions: a comparative analysis of machine learning models for predicting cricket player’s performance in the one day international (ODI) world cup 2023 J. Health Sport Rehab. 10 1 6 19This process is recursively applied to both subregions until the stopping condition is satisfied. Eventually, the input space is partitioned into M regions R and a decision tree (fleft(xright)) is generated, as shown in Eq. (16).Article
MATH
Google Scholar
MATH
Google Scholar
Sorry, a shareable link is not currently available for this article.iashchynskyi, P., & Liashchynskyi, P. Grid search, random search, genetic algorithm: a big comparison for NAS. arXiv preprint arXiv. 1912, 06059 (2019).
Methods and data
Data source
Article
Google Scholar
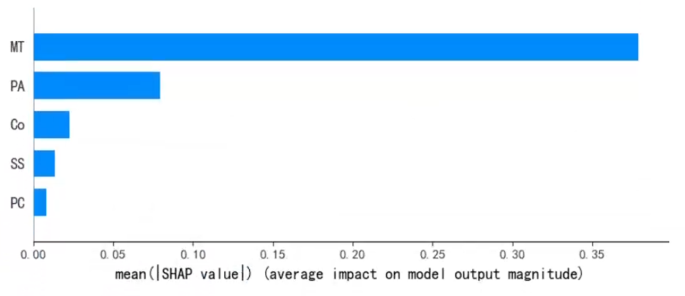
Average effect of SHAP values on model outputs.
Group environment questionnaire (GEQ)
Sports passion questionnaire (SPQ)
(a_i), (a_i^*) is the Lagrange multiplier and (kleft(x_i,xright)) is defined as the kernel function. There are a number of different kernels used to generate the inner product of the machine to be constructed in the input space. Different kernels will have different nonlinear decision surfaces and thus give different results. The kernel was chosen according to the characteristics of the input. In general, a common example of kernel function is Gaussian Radial Basis Function (RBF). In this paper, we also select RBF as kernel function, which is defined as follows Eq. (20).
Sports mental toughness questionnaire (SMTQ)
Athlete engagement questionnaire (AEQ)
The SPQ was compiled by Vallerand (2010)37. The use of Chinese athletes yielded favorable results in terms of reliability and validity. The scale comprises 16 items, encompassing three dimensions: general passion, harmonious passion and compulsive passion. The Cronbach’s alpha coefficient for this scale is 0.941, which meets the research requirements.
Machine learning model construction process
The RFR algorithm is an ensemble learning algorithm that combines multiple decision trees for prediction, and is particularly suited for handling high-dimensional and nonlinear complex datasets. This method effectively prevents data overfitting and allows for rapid training on test data. As shown in Fig. 1, the RFR algorithm consists of many decision trees, each constructed based on data samples from the training set. When performing regression tasks, the predictions from each tree are averaged to obtain the final prediction value. Typically, deep decision trees tend to overfit, but random forests can effectively mitigate this issue by training each tree with feature and sample subsets41. Features and samples were randomly selected from the input data, with each decision tree trained independently. The predictions of these trees were then aggregated to achieve more accurate predictions than a single decision tree model51.Article
ADS
CAS
MATH
Google Scholar
Machine learning model establishment process. This research employed Python version 3.9.1 and utilized the Sklearn library to construct a machine learning prediction model for athlete engagement. The specific methodology is outlined as follows:
Data collection and preprocessing
Therefore, the potential for implementing machine learning in sports is extensive. The application of machine learning in sports prediction offers significant opportunities for China to play a leading role on the global sports stage, having a profound impact on enhancing the overall competitiveness of the sports industry and advancing scientific excellence in sports.DW Ariani 2021 The relationship of passion, burnout, engagement, and performance: An analysis of direct and indirect effects among indonesian students J. Behav. Sci. 16 2 86 98In order to obtain sufficient data sets, this study distributed and collected questionnaires to athletes in multiple professional sports teams, high-level national training teams from Zhejiang, Heilongjiang, and Liaoning provinces by means of Wenjuanxing. From 1 June to 1 October 2021, a total of 445 questionnaires were distributed. Of these, 175 (53.7%) were male participants, a higher rate than females, and the average age of the athletes was between 17 and 22 years old and had about three years of training experience. Sports include: basketball (74), volleyball (36), soccer (63), cricket (47), ice hockey (20), curling (11), team aerobics (47) and others (28). All questionnaire surveys were conducted after sports training sessions. The questionnaire scale covered in this study can be divided into three parts: in the first part, we made it clear that the survey was based on the principles of voluntariness and anonymity; the responses to the questionnaire were used only for the researchers; they should not be used for any kind of profit or other purposes. The second part was to collect basic information about the athletes. In the third part, we set up the scales required for this study, including cohesion (Group Environment Questionnaire), passion (Sports Passion Questionnaire), mental toughness (Sports Mental Toughness Questionnaire) and athlete engagement (Athlete Engagement Questionnaire).
Written informed consent was signed by each team representative and all participants were informed that they could withdraw from the study at any time. All methods were carried out in accordance with relevant guidelines and regulations. This study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Ethics Committee of Zhejiang Normal University (ZSRT2022079).
Division of training set and test set
where (x_i) is an element of the training set, x is an element of the test set, and σ is a parameter of the RBF. However, the parameters of SVM are predetermined. Cross-validation is used to determine the parameter values. Whereas, SVM with fixed parameters are not applicable to changing athlete data.
Machine learning model algorithm test
The results of the SHAP analysis show that the three features cohesion, passion and mental toughness have a decisive influence on the predictions of model clearly. The data in Fig. 4 demonstrate the average SHAP values for the features Mental Toughness (MT), Passion (Pa), Cohesion (Co), Sports Satisfaction (SS) and Psychological Collectivism (PC), which visualise the average influence of each feature in the model predictions. It can be observed from the Fig. 4 that features MT, Pa and Co have higher average SHAP values, indicating that they occupy an significant position in model prediction. We further refine these to the level of a single sample, revealing the relationship between the feature values and their SHAP values for this sample which demonstrating the high prediction accuracy of the model by comparing the model predicted values with the actual values, as shown in Fig. 5. In this sample, the positive effect of feature MT is significant particularly, while the effects of features PC and SS are minor relatively. Combining the analyses in Figs. 4 and 5, we conclude that in the study sample, feature MT is the most critical factor influencing the prediction results of model, while features Pa and Co also have a significant impact. However, the impact of features PC and SS is weak relatively. These findings provide valuable information for an in-depth understanding of the decision-making mechanism of the model and also indicate the key features to focus on during data analysis and model optimisation.Article
Google Scholar
D Fletcher M Sarkar 2012 A grounded theory of psychological resilience in Olympic champions J. Psychol. Sport Exerc. 13 5 669 678
Feature selection of machine learning model
GBRT is an ensemble algorithm with a powerful learning strategy. Although it was initially designed to address classification problems, it has been successfully applied to the field of regression48. In the gradient boosting process, each step aims to minimize the loss function by adding elementary tree that reduce the loss function at each step, ultimately minimizing the loss function. In this way, GBRT is able to learn complex nonlinear relationships within the data.Y Kittichotsatsawat N Tippayawong KY Tippayawong 2022 Prediction of Arabica coffee production using artificial neural network and multiple linear regression techniques J. Sci. Rep. 12 1 14488
Output machine learning model prediction results
The regression tree ({h}_{m}(x)) is constructed by modeling ({z}_{m}(x)) and x. The weighting factors can be obtained by multiplying the importance of each feature by the corresponding coefficient of the model. Its formula is expressed in Eq. (12).
Machine learning model evaluation
H Liu W Hou I Emolyn Y Liu 2023 Building a prediction model of college students’ sports behavior based on machine learning method: combining the characteristics of sports learning interest and sports autonomy Sci. Rep. 13 1 15628
Xin Zhang and Zhikang Lin contributed equally to this work and should be regarded as co first authors.Article
MATH
Google Scholar
Machine learning algorithm theory
LR algorithm
D Chicco MJ Warrens G Jurman 2021 The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation J. PeerJ Comput. Sci. 7 623
MA Mohammed 2023 Adaptive secure malware efficient machine learning algorithm for healthcare data J. CAAI Trans. Intell. Technol. 2 1 12
KNN algorithm
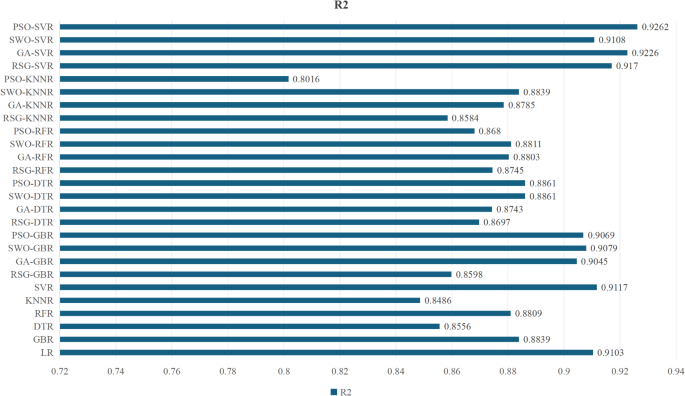
A Dorothea Wahyu 2021 The relationship of passion, burnout, engagement, and performance: an analysis of direct and indirect effects among Indonesian students J. Behav. Sci. 16 2 86 98Figure 7 displayed the prediction accuracy of regression models constructed using different machine learning algorithms. By comparing the R2 scores, the overall effectiveness of the different prediction models could be determined. The R2 score, also known as the coefficient of determination, is an important metric for evaluating the quality of regression models. It measures the extent to which the model explains the variability in the dependent variable, reflecting the accuracy of the model’s predictions. In model evaluation, a higher R2 score is preferred, indicating that the model fits the data better.
You can also search for this author in
PubMed Google Scholar
GBRT algorithm
Article
Google Scholar
CM Bishop NM Nasrabadi 2006 Pattern Recognition and Machine Learning Springer New York 738
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
You can also search for this author in
PubMed Google Scholar
DTR algorithm
In the construction of machine learning models, the RFECV method was used for feature selection. As an efficient wrapper-based feature selection technique, RFECV combined the advantages of Recursive Feature Elimination (RFE) and Cross-Validation (CV), enabling the automatic filtering of feature subsets that had the greatest impact on model performance.Article
Google Scholar
N represents the normalized data, X represents the measured value, ({X}_min) and ({X}_{max}) represent the minimum and maximum values, respectively.
The hyperparameters of the LR model include: copy_X (default True, prevents modification of the original data), fit_intercept (default True, calculates the intercept), n_jobs (default None, does not compute in parallel), and positive (default False, does not force the coefficients to be positive). For the optimal configuration of SWO combined with GBR, DTR, RFR and KNNR, the following hyperparameters are explained: in the GBR model, the learning rate is set to 0.1837, a lower value that helps the model to perform more fine-grained weight adjustments during the training process, thus improving the accuracy of the prediction; the maximum depth is 1.0, which indicates that we adopt a simpler tree structure to prevent overfitting; the number of estimators is 19.13, indicating that the predictive ability of the model is enhanced by adding more trees. In the DTR model, the optimal maximum depth is about 4.46, which helps the model to capture complex patterns in the data while avoiding the overfitting problem caused by too deep a tree structure. The number of estimators in the RFR model is 18.85, which indicates that the generalisation of model is enhanced by integrating more than one decision tree; the maximum depth is 37.85, which allows the model to learn more complex feature relationships; and the minimum sample leaf is 7.62, ensuring that the leaf nodes contain sufficient information. For the KNNR model, the optimal number of neighbours is 16, which indicates that the model makes predictions by considering the data points of the 16 nearest neighbours; the distance metric is set to “distance”, which indicates that the model takes into account the distances between the data points when calculating the predicted values.
Athlete engagement is influenced by several factors, including cohesion, passion and mental toughness. Machine learning methods are frequently employed to construct predictive models as a result of their high efficiency. In order to comprehend the effects of cohesion, passion and mental toughness on athlete engagement, this study utilizes the relevant methods of machine learning to construct a prediction model, so as to find the intrinsic connection between them. The construction and comparison methods of predictive models by machine learning algorithms are investigated to evaluate the level of predictive models in order to determine the optimal predictive model. The results show that the PSO-SVR model performs best in predicting athlete engagement, with a prediction accuracy of 0.9262, along with low RMSE (0.1227), MSE (0.0146) and MAE (0.0656). The prediction accuracy of the PSO-SVR model exhibits an obvious advantage. This advantage is mainly attributed to its strong generalization ability, nonlinear processing ability, and the ability to optimize and adapt to the feature space. Particularly noteworthy is that the PSO-SVR model reduces the RMSE (7.54%), MSE (17.05%), and MAE (3.53%) significantly, while improves the R2 (1.69%), when compared to advanced algorithms such as SWO. These results indicate that the PSO-SVR model not only improves the accuracy of prediction, but also enhances the reliability of the model, making it a powerful tool for predicting athlete engagement. In summary, this study not only provides a new perspective for understanding athlete engagement, but also provides important practical guidance for improving athlete engagement and overall performance. By adopting the PSO-SVR model, we can more accurately identify and optimise the key factors affecting athlete engagement, thus bringing far-reaching implications for research and practice in sport science and related fields.
RFR algorithm
J Bi 2023 PSOSVRPos: WiFi indoor positioning using SVR optimized by PSO Expert Syst. Appl. 222 119778
SVR algorithm
S Gu L Xue 2022 Relationships among sports group cohesion, psychological collectivism, mental toughness and athlete engagement in Chinese team sports athletes Int. J. Environ. Res. Public Health 19 9 4987
Suppose the training set (T={left(x_{1},{y}_{1}right),cdots ,left(x_{N},{y}_{N}right)}), (x_i) is the feature vector of an instance and ({y}_iin {{c}_{1},{c}_{2},cdot cdot cdot ,{c}_{n}}) is the class of that instance, (i =(text{1,2},cdot cdot cdot ,n)), for a test instance x, its class y can be represented in47 Eq. (8).
Stander, F.W., Leon, T. D. B., Stander, M., Mostert, K. & Coxen, L. A strength-based approach to athlete engagement: An exploratory study. J. South Afri. J. Res. Sport Phys. Educ. Recreat. 39, 165–175 (2017).
The choice of PSO-SVR over integrated learning is mainly based on its advantages in terms of interpretability, applicability to small datasets and strong generalization capabilities. This choice is suitable for scenarios particularly where accurate predictions need to be extracted from limited data. In contrast, integrated learning models tend to be more complex, demand higher computational resources, and may perform poorly when dealing with small sample data.
C Lonsdale K Hodge TD Raedeke 2007 Athlete engagement: I. A qualitative investigation of relevance and dimensions Int. J. Sport Psychol. 38 451 470
PSO-SVR algorithm
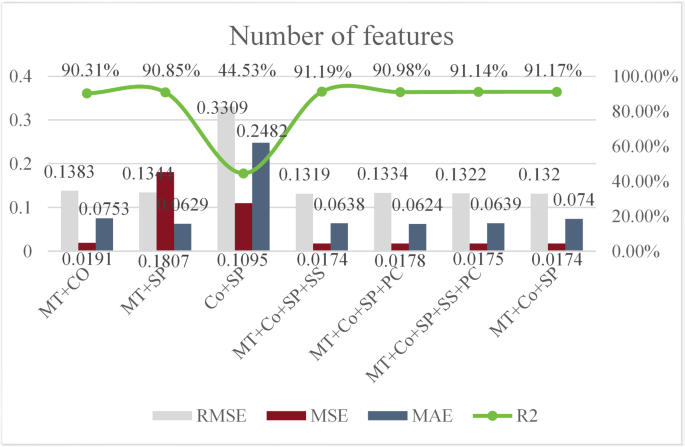
X Yizi 2024 Bioinformatics combined with machine learning to identify early warning markers for severe dengue J. China Med Univ. 53 7 583 590With the RFECV method, we successfully filtered the optimal feature subset for the machine learning model based on cohesion, passion and mental toughness. Figure 3 demonstrates that the model was effective in predicting athlete engagement using three feature subsets. These selected features comprised cohesion, passion and mental toughness, covering dimensions such as ATG-T, ATG-S, GI-T and GI-S; passion criteria, harmonious passion and obsessive passion; and confidence, constancy and control. The synergy of these features contributed to the model’s strong performance in predicting athlete engagement.
M Abdel-Basset R Mohamed M Jameel 2023 Spider wasp optimizer: A novel meta-heuristic optimization algorithm Artif. Intell. Rev. 56 11675 11738
Results
Model feature selection results
MATH
Google Scholar
MATH
Google Scholar
Algorithm for making predictions using random forest.

By considering the advantages and disadvantages of these algorithms and optimization strategies, we found that the SVR model combined with PSO performs the best in predicting athlete participation. The PSO-SVR model optimizes the parameters of the SVR through the PSO algorithm, which effectively improves the predictive performance of the model and reduces the risk of overfitting. Compared to other models, it performs better in handling nonlinear relationships and complex feature interactions. This result indicates that the PSO-SVR model has higher accuracy and stronger generalization ability in the task of athlete engagement prediction, which provides a valuable reference for future research and practice.where ({N}_{m}) is the number of samples in sub-region ({R}_{m}(j,s)). The data is divided into regions by selected ((j,s)) and the corresponding output values are determined as shown in Eq. (15).
Comparison of prediction models under different machine learning algorithms
where ({widehat{c}}_{m}) is the predicted value of the (m) th region and (I(xin {R}_{m})) is an indicator function to determine whether (x) belongs to region ({R}_{m}) . In this way, the decision tree can predict and analyze the data effectively.
As a core concept in the field of positive psychology, engagement refers to an individual’s persistent mental state filled with positive emotions, which is an important factor in influencing an individual’s behavioral performance and the direction of behavioral development. Although previous research in the area of sport performance has focused on burnout mostly as leading to maladaptation and sport dropout4,5. However, with the growth of the positive psychology movement, athlete engagement has received much attention and related research has become increasingly prominent6. Early identification of low-engagement individuals allows for intervention before the risk of burnout and disengagement occurs7. It needs to be specified that a state of non-burnout is not the same as engagement, and that low engagement is not burnout. Positive feedback can be obtained when we view athlete performance in a positive manner. Therefore, athlete engagement, as an important indicator of positive psychology of athletes, plays an important and positive role in improving athletes’ competitiveness and athletic performance. A high level of engagement is conducive to stimulating positive qualities that promote the development and maturation of athletes8, laying the foundation for enhancing their athletic ability9 and ultimately translating into significant improvements in athletic performance and achievement7.J Chuantong R Norsilawati Abdul R Nelfianty Mohd 2023 A Preliminary psychometric investigation of a Chinese version of athlete engagement questionnaire (AEQ) Int. J. Hum. Mov. Sports Sci. 11 1 103 111
In this study, we conducted a comprehensive analysis of the dataset with the aim of evaluating the applicability of different machine learning algorithms in constructing a prediction model for athlete participation based on their characteristics and advantages. We selected LR, KNN, GBRT, DTR, RFR, SVR and models combining four optimization algorithms (RGS, GA, SWO and PSO) to be trained and tested with the aim of identifying the most suitable models for predicting machine learning models for athlete engagement. During the course of our research, we found that each algorithm and its optimization strategy face unique challenges and potential limitations:
X Zhan S Zhang WY Szeto X Chen 2020 Multi-step-ahead traffic speed forecasting using multi-output gradient boosting regression tree J. Intell. Transp. Syst. 24 2 125 141
Process of adaption in SVR.
Google Scholar
Discussion
Sci Rep 15, 3220 (2025). https://doi.org/10.1038/s41598-025-87794-yYe, L. The Impacting Factors and Mechanism of Athlete Engagement. (D. Central China Normal University, 2014).MATH
Google Scholar
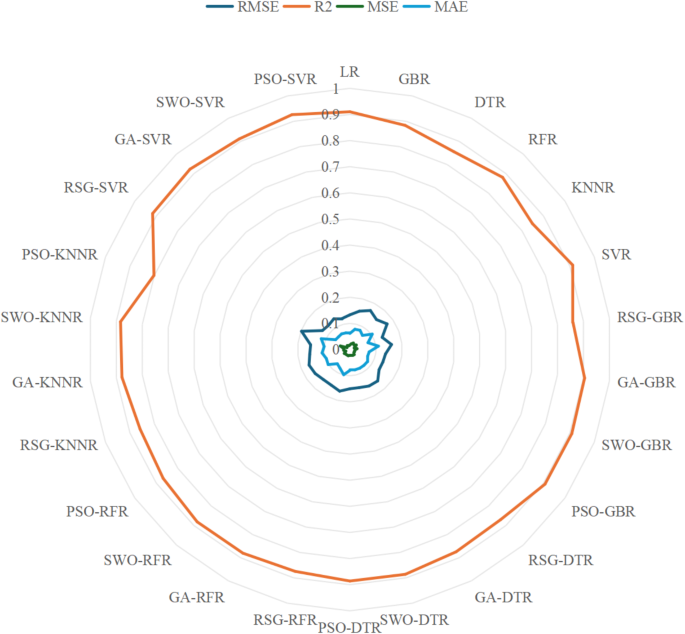
Radar plot of overall evaluation level of different machine learning algorithms.
Limitations and future research
PubMed Google Scholar
Conclusion
Data availability
RJ Vallerand 2010 On passion for life activities: The dualistic model of passion Adv. Exp. Soc. Psychol. 42 97 193
References
- where ({y}_i) is the truth value of the ith sample and (mathop ylimits_i left( {c_{m} ,g_{n} } right)) is a function of C and g. We terminate the optimization process when the predictive model yields the model we need.Houyuan, Z., Qi, Y., Shengren, C. & Bonan, Z. Research on prediction model of amateur runners’ sports performance based on FMS. C. Sports Biomech. Branch. 449–451 (2023).
- Article
Google Scholar
DF Gucciardi S Hanton S Gordon CJ Mallett P Temby 2015 The concept of mental toughness: Tests of dimensionality, nomological network, and traitness J. Personal. 83 1 26 44 - JM Keller MR Gray JA Givens 1985 A fuzzy k-nearest neighbor algorithm IEEE Trans. Syst. Man Cybern. 4 580 585This study aims to predict the level of athlete engagement by examining both team and individual dimensions. At the team level, cohesion is one of the most frequently cited concepts in sports science research. It refers to the solidarity and sense of belonging that individuals feel in a team, which is a key factor influencing team performance. Strong team cohesion predicts the level of athlete engagement. In sporting events, cohesion provides crucial social support for athletes23. Teams with high levels of cohesion usually result in higher levels of member engagement and increased support and trust in each other. Research suggests that cohesion is associated with satisfying psychological needs, promoting intrinsic motivation, and elevating athlete engagement levels. Increased team cohesion is an effective way to increase athlete engagement among athletes. It can be concluded that cohesion not only affects the emotional experience of athletes, but also plays an significant role in their behavioral performance. At the individual level9, passion and mental toughness play crucial roles in influencing athlete engagement. Hegel once asserted, “Nothing great in the world has ever been accomplished without passion.” Passion is not only a potential indicator of teacher engagement among secondary school24 but also significantly influences students’ learning engagement25. In sports, passion, internalized into personal identity26, fosters strong engagement, enabling athletes to persist in their activities. Research suggests that we should focus on promoting harmonious passion tendencies within achievement situations in order that there is an increased probability of adaptive behavioral outcomes ensuing and being able to promote healthy sport engagement27. Also, the two types of passion (harmonious and obsessive) should lead to engagement that, in turn, should lead to improved sport performance. Thus with passion, people are able to focus completely on the task at hand, give their full commitment to the sport, and experience positive results from their participation. Mental toughness is indispensable in both protecting and enhancing athlete engagement, representing a crucial psychological asset for achieving exceptional sporting performance. Research suggests that mental toughness is essential for athletes to cope with difficulties successfully, avoid the effects of stress and maintain their performance development28. It not only has a significantly positive predictive influence on athlete engagement29 but also correlates positively with an individual’s sports performance. Athletes with a high level of mental toughness can participate in the process of training and competing with a positive state of mind and body, and have a high level of athlete engagement (e.g., a high level of mental toughness). Athletes with high mental toughness have a strong degree of confidence in their own abilities and respond positively when they encounter difficulties, so they tend to approach training and competition with a more positive physical and mental condition30 and have a high level of athlete engagement. Therefore, mental toughness plays a central role in the foundation of sport success and is a proximal factor in the athlete engagement.
- DOI: https://doi.org/10.1038/s41598-025-87794-y
Google Scholar - SVR is a regression algorithm based on the Support Vector Machine (SVM) algorithm. SVR maps the input data to a high-dimensional feature space and constructs a hyperplane that maximizes the boundary between the predicted and actual values. In the given sample set (T={left(x_{1},{y}_{1}right),cdots ,left(x_{N},{y}_{N}right)}), there are N input variables (x_{t}) and corresponding output variables ({y}_{t},t=1,cdots ,N). The form of SVR can be expressed as follows Eq. (17).Different machine learning algorithms predict the outcome of the MAE.
- Xin Zhang & Song Guwhere (w) is an element in the high-dimensional space, (varphi left(xright)) is a nonlinear mapping function, and b is a threshold. Then, the above regression problem seeks to minimize the risk of f by minimizing the Euclidean norm of w to reduce the complexity as follows Eq. (18).
- Different machine learning algorithms predict the outcome of R2.Supervised learning models can be classified into regression and classification techniques when used to predict continuous and discrete target variables. LR is a typical regression model that predicts targets through the following equation45 . Its formula is expressed in Eq. (7).
- Previously, researchers have delved into the factors affecting athlete performance from a number of perspectives, encompassing not only the traditional technical, tactical and physical aspects, but also cutting-edge areas such as exercise fatigue, recovery mechanisms and psychological factors. Therefore, analyzing and predicting athlete performance is a complex and dynamic endeavor that involves multiple considerations. And machine learning technology plays an important role in analyzing data on athlete performance. The application of this technology is changing the way athletes are monitored in terms of health and performance, thus impacting their training, competition and career management. However, in previous studies, many researchers and coaches have focused on reducing exercise fatigue and burnout, so that they overlooking the fact that athletes who maintain a high level of engagement with training and competition are the ones who respond positively to the stress of competition and perform well in training or competition. Engagement represents a sustained, shared affective-cognitive state of concentration on any object, event, person or behavior. When athletes have a sense of control over their ego state, it helps them achieve their goals. Athlete engagement studied in this paper serves as an important indicator of positive athletic performance and can reflect positive and healthy mental states of athletes. Athletes’ mental health is a major resource throughout their athletic career and beyond. However, the diversity and complexity of sports performance and the nonlinear relationships between psychological traits complicate the task of analysis and prediction using traditional methods. Therefore, the use of effective machine learning models may help to achieve highly accurate predictions of athletic performance.K Goodger T Gorely D Lavallee C Harwood 2007 Burnout in sport: A systematic review J. Sport Psychol. 21 127 151
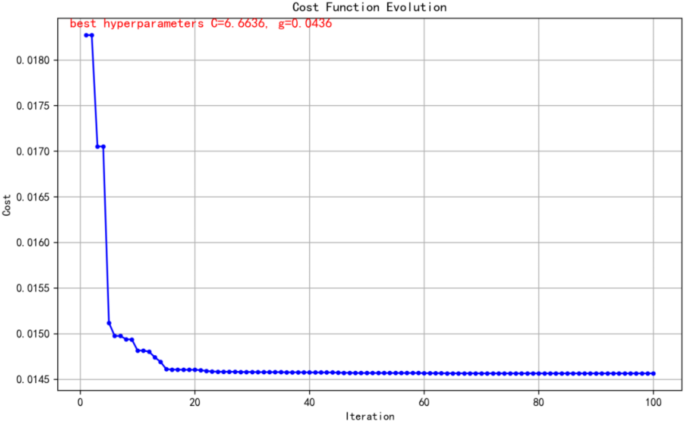
- Through Table 3, the pso-SVR model was identified as the best hyperparameter combination. As shown in Fig. 6, the best hyperparameters for this machine learning model with respect to the features of cohesion, passion and mental toughness were C = 6.6636 and g = 0.0436. With this hyperparameter combination, the model achieved a prediction accuracy of 92.62%, demonstrating its effectiveness in predicting athlete engagement.Here ({(j,s)}^*) represents the selected best feature (j) and the cut point (text{s}), while ({R}_{1} (j,s)) and ({R}_{2} (j,s)) denote the two subregions obtained after the cut respectively. ({y}_i) is the target value of the ith sample, ({c}_{1}) and ({c}_{2}) are the average of the target values in the two subregions, which are calculated using the formula in Eq. (14).
- C Lonsdale K Hodge S Jackson 2007 Athlete engagement: II. Development and initial validation of the athlete engagement questionnaire Int. J. Sport Psychol. 38 4 471 492This study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Ethics Committee of Zhejiang Normal University (ZSRT2022079). All methods were carried out in accordance with relevant guidelines and regulations. Informed consent has been obtained from the participants. We express our great gratitude to all the authors of the scales and all the participants in the present study.
- RFE is a feature selection technique that relies on a specific machine learning model to achieve a predefined number of features by iteratively eliminating features with lower weights. It sorts features based on the model’s coefficient weights or importance scores, recursively removing a certain proportion of redundant or irrelevant features at each iteration, ultimately retaining the subset of features that contributes most to the model’s predictive capability. However, a limitation of the traditional RFE method is the need to manually set a threshold for retaining the number of features, which could lead to the loss of important features or the retention of unnecessary ones. To overcome this drawback, this study adopted RFECV. This method evaluates the performance of each feature subset and selects the feature combination with the highest score, thereby ensuring that the chosen feature subset maximizes its contribution to model performance and effectively avoids the accuracy loss that may result from manually setting thresholds43. Using the RFECV method, we screened out features with higher weights and determined that the three features of cohesion, passion and mental toughness were critical for model performance by comparing different combinations of features, as detailed in Table 2.AC St-Louis M Rapaport PL Chénard RJ Vallerand S Dandeneau 2021 On emotion regulation strategies and well-being: The role of passion J. Happiness Stud. 22 1791 1818
- T Zhou L He J Wu F Du Z Zou 2019 Prediction of surface roughness of 304 stainless steel and multi-objective optimization of cutting parameters based on GA-GBRT J. Appl. Sci. 9 18 3684AV Carron P Chelladurai 2010 The dynamics of group cohesion in sport J. Sport Psych. 3 2 123 139
- MATH
Google Scholar - Feature selection of machine learning model. The study decided to select the features for the machine learning model from the athletes’ cohesion, passion and mental toughness. Cohesion consists of four scores: ATG-T, ATG-S, GI-T and GI-S; Passion consists of three scores: passion criteria, harmonious passion and obsessive passion; Mental toughness consists of three scores: confidence, constancy and control.
Google Scholar - Article
Google Scholar
Article
Google Scholar - Article
Google Scholar - To validate the performance of the model, the available database was divided into two distinct groups: a training set for training predictive models and a testing set for evaluating its performance. After comparing the experimental results of different data partition ratios, we found that the 8:2 partition ratio has the lowest RMSE, as detailed in Table 1. During the model training phase, we improve the parameters continuously and use the test set to evaluate the performance of the model for further refinement. The test set not only evaluates the data, but also confirms the reliability and generalization ability of the model. In addition, employing five-fold cross-validation35, we guarantee the ability of model to generalize and successfully mitigate the danger of overfitting.Article
MATH
Google Scholar - JA Segovia JF Toaquiza JR Llanos DR Rivas 2023 Meteorological variables forecasting system using machine learning and open-source software J. Electron. 12 4 1007Article
Google Scholar - Zhang, L. W. & Mao, Z. X. Evaluation Manual of Psychological Scales Commonly Used in Sports Science. J. Beijing Sports Univ. Press. 378, 7-81100-226-4 (2004).
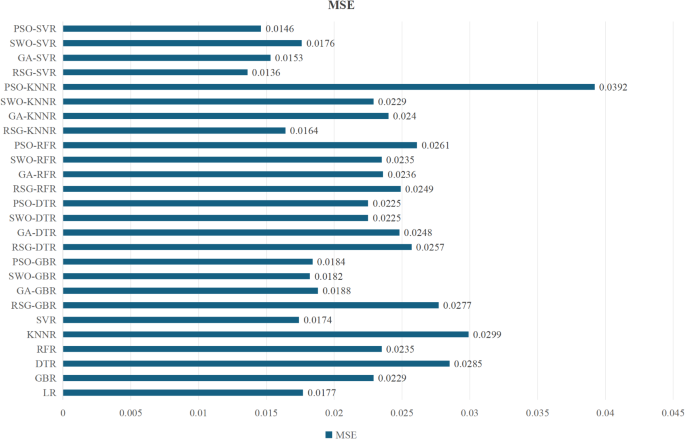
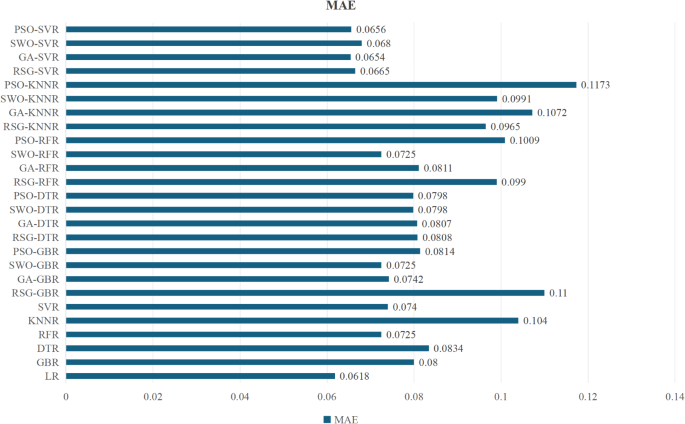
- M Sheard J Golby A Wersch van 2009 Progress toward construct validation of the sports mental toughness questionnaire (SMTQ) Eur. J. Psychol. Assess. 25 3 186 193 https://doi.org/10.1027/1015-5759.25.3.186Figures 9 and 10 displayed the MSE and MAE of seven machine learning algorithms. Both MSE and MAE were crucial indicators for assessing model quality, directly reflecting the accuracy of the model’s predictions. By comparing these error metrics, the overall effectiveness of the different prediction models could be determined. Before assessing model performance, lower MSE and MAE values indicated that the model’s predictions were closer to the actual data. Based on the results in Fig. 9, we can see that the PSO-SVR model has the best performance with an MSE of 0.046. This is followed by the GA-SVR model with an MSE of 0.0153. The LR model has an MSE of 0.0177. According to the results in Fig. 10, the LR model has an MAE of 0.0618 which is the best performance. This is followed by the PSO-SVR model with an MAE of 0.0656. The MAE of the RFR model was 0.0708, while the MSE and MAE values of the other four algorithms were higher, indicating larger prediction errors. Therefore, based on MSE and MAE values, the PSO-SVR model demonstrated the best performance in predicting athlete engagement, with the lowest error metrics, meeting the research requirements. This suggested that the PSO-SVR model was more effective in predicting athlete engagement while maintaining lower prediction errors.
- Data preprocessing and normalizing techniques are employed to enhance the dataset’s quality. These methods aim to optimize the performance of machine learning algorithms by minimizing data noise and decreasing data dimensions42. The input dataset comprises the cumulative scores for cohesion, passion and mental toughness, whereas the output dataset comprises the overall score for athlete engagement. Input and output data normalized in the range 0 to 1. Equation (1) was used for normalization of data.
Google Scholar - W Zhaohua L Jie W Bo D Nana N Fuhua 2024 Research on mining and applications of individual heterogeneity factors in resident demand response by integrating machine learning and SHAP value algorithm J. Syst. Eng. theory Pract. 44 7 2247 2259Correspondence to
Song Gu. - S Kent K Kingston KF Paradis 2018 The relationship between passion, basic psychological needs satisfaction and athlete burnout: Examining direct and indirect effects J. Clin. Sport Psychol. 12 75 96Optimal hyperparameters for machine learning feature models.
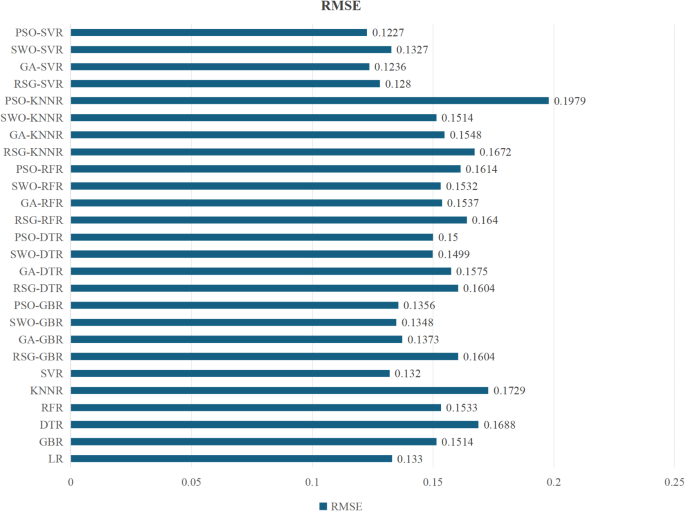
- In sports, the application of machine learning and AI technologies is continually broadening the boundaries of sports talent development, athlete performance enhancement and event decision-making. Through these advanced technologies, coaches and sports teams are able to achieve accurate predictions of athlete performance, driving a shift in the decision-making process from intuitive experience to quantitative data-based analysis10. Researchers have used smart technologies to play an significant role in several aspects of selection of basketball players, analysis of game activity, prediction of results and so on, improving team competitiveness significantly11,12. The soccer club case further demonstrates the practical application of sports data analytics in predicting injury prevention, assessing optimal performance and optimizing training13. It is clear that predictions utilizing machine learning that enable timely assessment of athletes’ reaction and performance to different scenarios are critical for improving skills, promoting team synergy and guiding sports teams towards success. This highlights the significant value of sports prediction modeling in contemporary sports.Table 1 presented a summary of the predictive accuracy, RMSE, MSE and MAE of the prediction models constructed using seven different machine learning algorithms. Figure 11 displayed a radar chart generated from Table 3, which was used to assess the overall effectiveness of the prediction models established by these algorithms. To visually compare the performance of the different machine learning algorithms’ prediction models in terms of statistical accuracy, the radar chart was used to show the models’ combined performance across four dimensions: RMSE, MSE, MAE and predictive accuracy. In this radar chart, PSO-SVR and LR perform well on all assessment metrics, especially their R2 values are close to 1, showing high predictive accuracy. Although GBR performs well on R2, its RMSE and MSE are not as good.
- Article
PubMed
PubMed Central
MATH
Google Scholar
where ({|left|wright||}^{2}) is the Euclidean norm of the weight vector, which is used to control the complexity of the model. ({R}_{reg}) is the empirical risk, (C) is the penalty parameter used to balance the weights of the descriptive function and the empirical risk, and ({left|{y}_i-fleft(xright)right|}_{varepsilon }) is the insensitive loss function used to measure the difference between the predicted value (fleft(x_iright)) and the true value ({y}_i). By introducing the non-negative slack variable ξ and the Lagrangian function, the function (fleft(xright)) is described as follows using the Karush–Kuhn–Tucker (KKT) condition Eq. (19). - Article
Google Scholar
AB Mahmoud WD Reisel A Berman L Fuxman 2024 Unlocking athletic potential: Harnessing people analytics for optimal performance and talent management in sports A Mansurali P Mary Jeyanthi D Hack-Polay AB Mahmoud Eds Sports analytics: Data-driven sports and decision intelligence Springer Nature Switzerland Cham - The study was funded by Zhejiang Provincial Philosophy and Social Sciences Work Office, 23NDJC118YBThis study comprehensively considered key characteristics such as cohesion, passion and mental toughness, and developed a machine learning model aimed at predicting athlete engagement. Through an in-depth comparison and analysis of the six base algorithms and four optimization algorithms, we observe that the PSO-SVR model outperforms the other models in terms of prediction accuracy significantly. In particular, it has demonstrated a remarkable ability to deal with non-linearities, adapt and optimize the feature space, and provide more accurate and reliable predictions of athlete engagement. The PSO-SVR model performed impressively in predicting athlete engagement with a prediction accuracy of 0.9262. In contrast, other models such as GA-SVR, RGS-SVR, SVR, LR and SWO-GBR are less predictive slightly. The results of this research not only highlight the great potential of the PSO-SVR model in predicting athlete engagement, but also provide a solid scientific basis for the field of athletic training and management. In summary, the wide application of the model is expected to provide scientific decision support in the field of sports training and management, and thus improve the individual performance of athletes and the overall competitiveness of sports teams.
- LR struggles to capture the complex nonlinear relationships of psychological features and has limited predictive power. KNN has reduced accuracy on small datasets and is sensitive to feature scaling. GBRT and DTR are susceptible to overfitting by noise and outliers. RFR performs poorly when dealing with highly correlated features. SVR has stringent kernel function selection and preprocessing requirements. RGS is computationally expensive in high dimensional spaces. GA requires fine tuning of parameters and multiple iterations to converge31,32. SWO as a new algorithm, lacks empirical guidance for parameter tuning and may not be as effective as mature algorithms33. PSO is easy to fall into local optimum in high dimensional space, and is very sensitive to the initial setting and parameter adjustment34.ZA Sejuti MS Islam 2023 A hybrid CNN–KNN approach for identification of COVID-19 with 5-fold cross validation J. Sens. Int. 4 100229
- MATH
Google Scholar - C Tedi 2023 Coach leadership style, coach-athlete relationships and engagement in team sports: The mediating role of athlete burnout Revista iberoamericana de psicología del ejercicio y el deporte. 18 5 687 692The SMTQ was compiled by Sheard, Golby and Wersch (2009)38. The Chinese version of the questionnaire demonstrated good reliability and validity in its application within China. There are 14 items in total, including three dimensions of self-confidence, constancy and control. A higher score indicates greater mental toughness in the athlete. The Cronbach’s ɑ coefficient for the questionnaire in this study was 0.849, signifying its strong reliability.
- As an algorithmic discipline, machine learning analyzes and assimilates large volumes of pre-existing or synthesized datasets to make predictions and assessments. This provides sports scientists, coaches and athletes with an objective analysis tool for evaluating their performance, thus assisting them in making optimal decisions. Through personalized predictions from “learning algorithms”, it is possible to conduct in-depth analysis of each athlete’s performance and develop customized training plans to help them achieve optimal athletic performance. This allows athletes to gain a more comprehensive understanding of their physical and mental health, enabling timely adjustments and improvements in their performance during training and competitions. Coaches, for their part, can use predictive modeling to monitor athletes engagement levels regularly. Based on the prediction results, real-time information on the athlete’s true athletic performance can be obtained, and measures can be taken timely, such as adjusting the training load or adding psychological counseling. Changes in athlete engagement before and after training can also be analyzed to assess the effectiveness of training interventions and optimize future training strategies continuously. Such data-driven decision-making is often more reliable than subjective judgment. Sports managers can leverage insights from machine learning research to better support coaches and athletes, optimize resource allocation, and enhance the overall competitiveness of sports teams or programs. For example, predictive modeling of athletic engagement is utilized to develop scientific selection criteria to ensure that athlete reserves are recruited that match the team’s culture; Counseling and support resources can be allocated according to the psychological needs of athletes to ensure that athletes receive the support they need during training and competition.
- In the field of sports, the utilization of machine learning technology has become a key strategy for data exploration and extraction, leveraging its interdisciplinary nature to integrate the advantages of sports science, computer science and statistics. This field not only demonstrates multi-layered and multi-domain characteristics but also highlights the importance of data analysis in specific training and competition scenarios, reflecting the overall trend toward precise sports training and management52. Big data analysis in the field of physical activity using AI techniques is justified as one of the important and effective tools to improve the quality of health and sports performance of professional athletes. As a fundamental application of artificial intelligence, machine learning, with its integration of various interdisciplinary domains and excellent performance, has emerged as a prominent topic in sports training method research.
- MATH
Google Scholar
The GEQ compiled by Carron (2010) and translated by Ma Hongyu36 was adopted. This questionnaire represents a specialized tool for assessing cohesion in sports, which has good reliability and validity in Chinese use. The questionnaire comprises 15 items, encompassing the dimensions of Attraction to Group Task (ATG-T), Attraction to Group Social (ATG-S), Group Interaction Consistency (GI-T), and Group Social Interaction Consistency (GI-S). The Cronbach ɑ coefficient of test–retest reliability is 0.869, which meets the needs of this study. - Faculty of Information Science and Technology, Zhongkai University of Agriculture and Engineering, Guangzhou, 510225, ChinaDownload citation
- In order to determine the best technology, we use the Root Mean Square Error (RMSE), Mean Square Error (MSE), Mean Absolute Error (MAE) and coefficient of determination (({R}^{2})) as evaluation indicators41. In the following formula, ({X}_i) represents the predicted value of the (i) th element, while ({Y}_i) denotes the actual values of the (i) th element. The regression method forecasts the ({Y}_i) value corresponding to the ({X}_i) value in a real dataset. The average of the true values44. Its formula is expressed in Eq. (2).Zhikang Lin
- Article
Google Scholar - Given that athletes might be affected by various circumstances, including physical exhaustion and meteorological conditions. These factors may lead to noise or fluctuations in the statistics. By calculating an average of every 8 data points, the impact of short-term variations can be reduced effectively and unwanted noise is minimized. This facilitates the observation of long-term trends and alterations. In some cases, athlete data may show higher densities, complicating analysis. High frequency data can be reduced to lower frequencies to make the analysis process more efficient41. Data preprocessing is an essential step in tailoring the dataset to meet the unique requirements of various machine learning algorithms. It plays a pivotal role in assessing the predictive capabilities of different models.Our goal is to determine a function, (Fleft(xright)), which minimizes a specific loss function (L(y,Fleft(xright))). GBRT approaches the optimal solution (widehat{F}(x)) step by step by weighted combination of these simple regression trees (h(x_{t})). In GBRT, each basic regression tree (h(x_{t})) is constructed based on the input variable X and the negative gradient of the loss function. Together, these trees allow the model to capture the complex nonlinear relationships in the data more accurately. The model is formulated as follows49 Eqs. (9) and (10).
- Machine learning-based predictive models do show great potential in providing personalized strategies for athlete training and enhancing athlete engagement. However, this predictive model faces a number of challenges. For example, the PSO algorithm may encounter the problem of local optimal solutions when applied, the choice of algorithm parameters has a significant impact on the final results, and also its search efficiency may decrease when dealing with high-dimensional feature spaces. At the same time, the PSO-SVR model’s dependence on self-reported data may lead to biased predictions, as these data are often influenced by the subjective feelings of individual athletes. In addition, data privacy and security issues are critical when deploying models. We need to take measures such as data desensitization and encryption to protect the privacy of research subjects and to improve model transparency and interpretability.Reprints and permissions
- Anyone you share the following link with will be able to read this content:Selection of cross-validation scores based on machine learning feature models.
- As for the combination of PSO and SVR, the following is an explanation of the optimal configuration of the hyperparameters: the regularization parameter C was set to 6.66, a choice that highlights the fact that we struck a good balance between model complexity and training error. This aims to prevent model overfitting while ensuring the model’s ability to fit the training data efficiently; the coefficient of the kernel function is 0.0436, and this low gamma value implies that the model prefers to use smoothed decision boundaries, which helps to capture the overall structural characteristics of the data; and the kernel type is chosen to be “rbf”, the radial basis function kernel, which specializes in revealing nonlinear relationships in the data, which is essential for enhancing the predictive power of the model. By carefully optimizing these key hyperparameters, the prediction accuracy of the SVR model is significantly improved. This makes it stand out in the comparison of many optimization algorithms and show excellent performance.Regarding the predictive accuracy of various models, the PSO-SVR model achieved the highest accuracy at 92.62%. The variables chosen to represent this study are cohesion, passion and mental toughness, which are significant potential factors influencing athlete engagement, although other factors may also affect their engagement. The PSO-SVR model excels in handling cohesion, passion and mental toughness due to its adaptability to data features and patterns, strong ability to handle high-dimensional features, and effectiveness in managing small samples and category imbalances.
- Article
Google Scholar
The authors declare no competing interests. - Different machine learning algorithms predict the outcome of the RMSE.The AEQ was compiled by Lonsdale et al.39(2007) and revised by Ye Lv’s translation29. The questionnaire comprises 16 items, encompassing the four dimensions of self-confidence, dedication, vigor and enthusiasm. A higher score indicates a greater level of engagement from the athlete. The Cronbach’s alpha coefficient for this scale is 0.959, which meets the research requirements.
- Machine Learning Model Prediction Results and Key Characterization.
- G Aurélien 2017 Hands-on machine learning with scikit-learn & tensorflow Geron Aurelien 134 145 150Received:
- Overall results indicated that the PSO-SVR algorithm performed the best in terms of accuracy, and RMSE and MSE scores are relatively low (see Table 3). It can be concluded that this model not only has high predictive accuracy but also exhibits low prediction errors. Compared to PSO-SVR, the LR algorithm has lower accuracy. However, LR outperforms PSO-SVR in terms of MAE, possibly because the errors in LR are symmetrically distributed, whereas the increased complexity of PSO-SVR may result in asymmetric error distribution. GA explores the solution space in depth through crossover and mutation so that better Mae metrics can be found. The stochastic nature of RSG can be an advantage in complex parameter spaces, especially when optimizing MSE.Different machine learning algorithms predict the outcome of the MSE.
- Article
Google Scholar
Alibrahim, H. & Ludwig, S. A. Hyperparameter Optimization: Comparing Genetic Algorithm against Grid Search and Bayesian Optimization. In 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 1551–1559 (2021). - H Zhaorigetu 2022 Prediction of sports performance combined with deep learning model and analysis of influencing factors J. Sci. Program. https://doi.org/10.1155/2022/4082906N Louw SJ Steel 2006 Variable selection in kernel Fisher discriminant analysis by means of recursive feature elimination J. Comput. Stat. Data Anal. 51 3 2043 2055
- S Kannappan 2023 Perceived organizational support and employee engagement: Mediating role of work passion of the employees Manag. Br. J. Adm. Manag. 58 156 210 212Article
MathSciNet
MATH
Google Scholar - Article
ADS
CAS
PubMed
PubMed Central
Google Scholar
Machine learning, a powerful interdisciplinary technology that incorporates multiple disciplines, has the remarkable capability to learn autonomously from experience.It constructs predictive models using “learning algorithms” to make accurate, personalized predictions for new scenarios. As a core component of artificial intelligence, machine learning plays a vital role by extracting valuable insights from diverse and complex data sets. Its applications extend to numerous fields, including medicine1, bioinformatics2 and automation technology3. - Article
MATH
Google Scholar
JO Emily H James M David 2010 Identifying important practice behaviors for the development of high-level youth athletes: Exploring the perspectives of elite coaches J. Psychol. Exerc. 11 6 433 443 - College of Physical Education and Health Sciences, Zhejiang Normal University, Jinhua, 321004, ChinaIn this study, RFECV was employed to identify the optimal number of features for the model. The input features considered included mental toughness, cohesion, passion, sports satisfaction and psychological collectivism.
- To assess the predictive performance of each model, four types of metrics were used: RMSE MSE, MAE and ({R}^{2}).
M Sorkkila A Tolvanen K Aunola TV Ryba 2019 The role of resilience in student-athletes’ sport and school burnout and dropout: A longitudinal person-oriented study Scand. J. Med. Sci. Sports 29 7 1059 1067
Acknowledgements
Funding
Author information
Authors and Affiliations
Contributions
Corresponding author
Ahmed, N. Understanding Sports Data Analytics Simplified. Hevodata. Saatavilla: https://hevodata.com/learn/sports-data-analytics/. (2022).
Ethics declarations
Competing interests
The coefficient of determination ({R}^{2}), is used to quantify the extent to which the predictive model can capture variations in outcomes and to determine which model excels in fitting the data. The calculation of R squared is described by Eq. (3). The preferred metric, as illustrated in Eq. (4), is the RMSE, a quantitative measure used to evaluate the effectiveness of regression models. It quantifies the average of the squared differences between the observed and predicted values of the target variable. A lower RMSE value indicates superior model performance, signifying a smaller average deviation between the predicted and actual values. Additionally, as calculated in Eq. (5), the MSE can be included as a complementary metric, which measures the average of the squared errors in a set of predictions. The last metric is the MAE, which quantifies the differences between observed and predicted values, providing a measure of the typical error magnitude. It is calculated according to Eq. (6), where m represents the sample size, ({Y}_i) denotes the actual values, and (widehat{{Y}_i}) represents the forecasted values.
Additional information
Publisher’s note
This study develops and compares several prediction models, including Linear Regression (LR), k-Nearest Neighbors (KNN), Gradient Boosting Regression Tree (GBRT), Decision Tree Regression (DTR), Random Forest Regression (RFR) and Support Vector Regression (SVR). To enhance the predictive capabilities of these base models, we employ four efficient optimization algorithms: Random Grid Search (RGS)31, Genetic Algorithm (GA)32, Spider Web Optimization (SWO)33 and Particle Swarm Optimization (PSO)34. Additionally, to ensure the model’s reliability and robustness, we utilize five-fold cross-validation35 to assess the model’s stability. Through these integrated methods, the study aims to evaluate the accuracy, stability, and overall performance of the models in predicting athlete participation.
Rights and permissions
PubMed
Google Scholar
DTR is both an effective classification method and a commonly used technique in regression analysis. As a fundamental machine learning algorithm, it is characterized by strong self-learning capabilities, good model interpretability and high learning efficiency50. The structure of a decision tree consists of leaf nodes, branches and a root node. It integrates all variables, subdivides nodes into child nodes, and selects the splitting method that generates the most homogeneous child nodes during this process, with predictions determined by the path leading to the leaf nodes. DTR is not only easy to learn and understand but also directly visualizable. It constitutes one of the most direct methods for revealing key interactions between variables.
About this article
Cite this article
The KNN algorithm is applicable not only to classification tasks but also to regression tasks. In regression tasks, the goal is to predict continuous values rather than discrete labels as in classification tasks. Specifically, for each test sample to be predicted, its predicted value is determined by examining the k nearest neighbors found in the training set and averaging the values of these neighbors.L Yang A Shami 2020 On hyperparameter optimization of machine learning algorithms: Theory and practice J. Neurocomput. 415 295 316